Magnetism, superconductivity and their coexistence in KTO 2DEGs
New, high quality materials can often mean new functionality and new physics. In our group we explore these materials using low noise, low temperature transport techniques, which can give us an insight into the mechanisms behind the observable phenomena. Earlier, we focused on epitaxially grown LaAlO3 / SrTiO3 (LAO-STO) interfaces, which showed a number of interesting effects such as the coexistence of superconductivity and magnetism and strongly anisotropic transport. More recently, our focus has been on two dimensional electron gases (2DEGs) at the surfaces of the complex oxide KTaO3 (KTO). KTO is similar in many ways to STO: it is a cubic perovskite at room temperature, although it does not undergo a cubic to tetragonal structural transition like STO at lower temperatures; it is a quantum paraelectric, with a dielectric constant that grows with decreasing temperature (but not as large in magnitude as in STO); and most importantly, one can create a 2DEG on the surface of KTO or at its interfaces with other materials.
Like STO, KTO has intrinsic spin-orbit interactions, but the spin-orbit interactions are about a factor of 20 larger in KTO than in STO. Also like STO, superconductivity has been discovered in KTO 2DEGs but at temperatures almost an order of magnitude larger than in STO 2DEGs, which is a bit surprising, as bulk KTO does not show superconductivity when doped, unlike STO. In addition, the superconductivity in KTO 2DEGs is strongest in the (111) surface crystal orientation, being almost absent in the (100) surface crystal orientation.
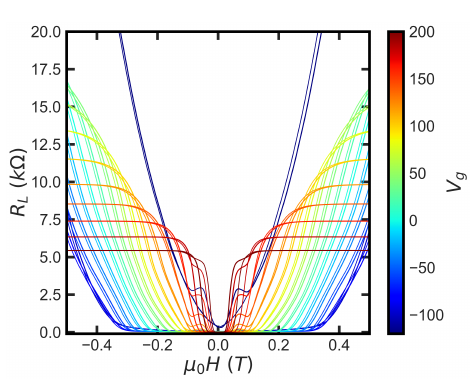
We fabricate KTO 2DEGs by evaporating and then oxidizing a thin layer of Al on the KTO surface. Al getters oxygen from the KTO surface, creating oxygen vacancies which render the KTO surface conducting. The 2DEG can have either a (001), (110) or (111) orientation, which determines the symmetries of the resulting 2DEG band structure. We discovered that the resulting 2DEG is magnetic, showing hysteresis in its magnetoresistance (MR), and that this magnetism coexists with superconductivity. Figure 1 shows the MR of a (111) oriented KTO 2DEG at 30 mK at various values of the back gate voltage Vg .
Near zero magnetic field, the resistance vanishes for large negative values of Vg, but the resistance becomes finite for magnetic fields greater than ~0.3 T. As Vg increases, the field range over which the device remains in the zero resistance state decreases, and the MR becomes clearly hysteretic, indicating the presence of ferromagnetic order in the sample.
Berry dipoles and the nonlinear Hall effect in KTO 2DEGs
The strong spin orbit interactions in KTO enable the exploration of potential topological effects. Since the KTO crystal has time reversal symmetry in zero external magnetic field, the net Berry flux vanishes, but the Berry curvature need not vanish. Indeed, DFT calculations by our collaborators in Professor Pallab Goswami’s group at Northwestern University show that the surface bands do indeed have finite Berry curvature. Figure 2(a) shows the dispersion of the surface bands calculated for the (111) surface orientation. The Berry curvature of these bands for the cut taken along μ1 in Figure 2(a) is shown in Figure 2(b) along the surface crystal momentum directions. The Berry curvature is antisymmetric in the momentum. An antisymmetric Berry curvature raises the possibility of a so-called Berry dipole. For the (111) crystal surface orientation of KTO, the net Berry dipole vanishes, but it does not vanish for the (110) crystal orientation.
Since it preserves time reversal symmetry, KTO is not expected to show a spontaneous Hall effect in zero magnetic field, but the presence of a Berry dipole moment implies that it may show a nonlinear Hall effect.
Figure 3. Schematic of the experimental configuration to measure the nonlinear Hall effect.
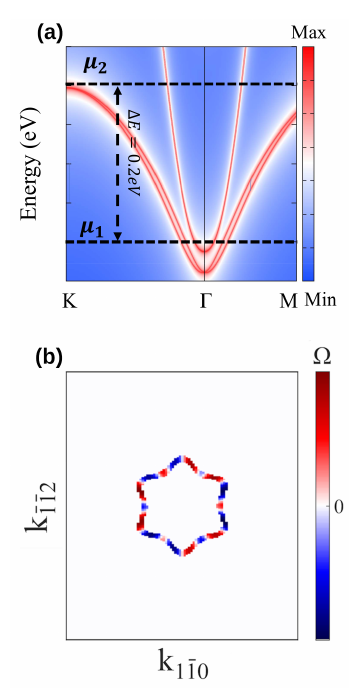
Figure 3 shows the experimental schematic to measure the nonlinear Hall effect in a six-terminal Hall bar configuration defined on the surface of a KTO crystal. An ac current is applied along the length of the Hall bar, and the longitudinal and transverse voltages (or equivalently, resistances) are measured as a function of the back gate voltage Vg as well as a dc voltage VT (or current) applied across the transverse contacts. Applying VT (or IT) shifts the Berry curvature, and is predicted to give rise to a finite Hall voltage when measured at the second harmonic of the longitudinal ac current.
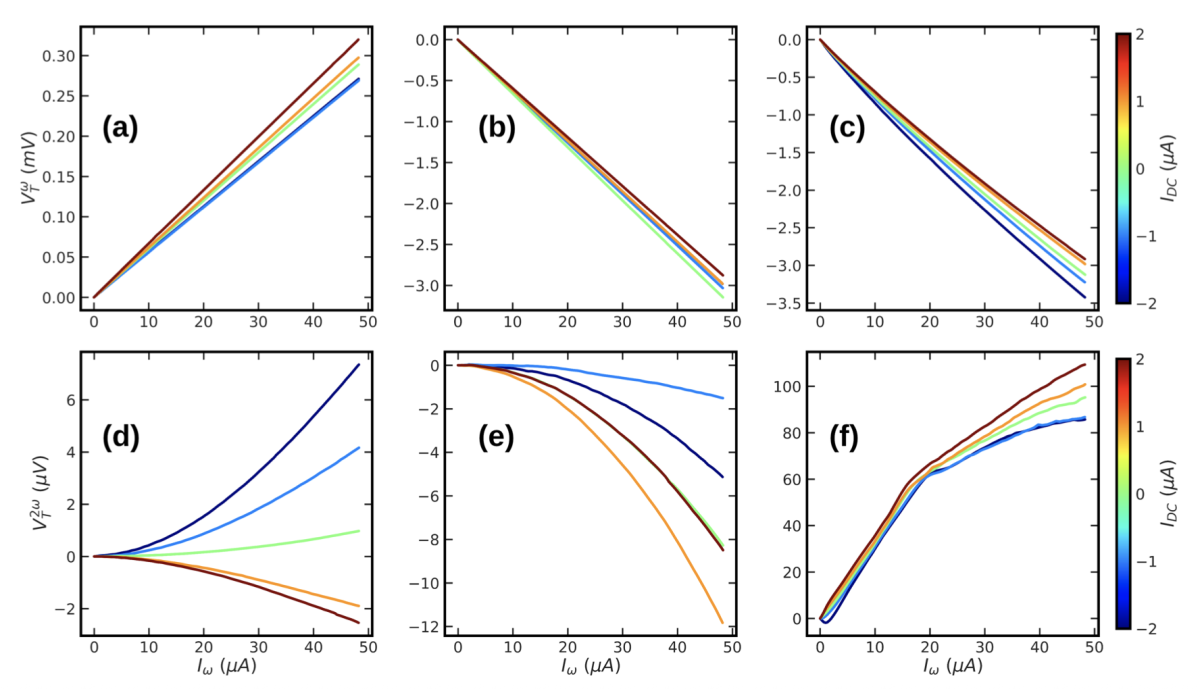
Figure 4 shows the first and second harmonic of the transverse voltage measured as a function of the ac drive current for various values of a transverse dc current. The three columns correspond to the (100), (110) and (111) crystal orientations. For all three orientations, the first harmonic response varies only weakly with the transverse dc current while the second harmonic response varies strongly, even changing sign for the (100) orientation . The second harmonic response for the (110) orientation is about a factor of 2 larger than that for the (100) orientation, but the second harmonic response for the (111) sample is almost a factor of 10 larger than the response for the (100) orientation. This is surprising as theoretically, only the (110) surface crystal orientation should show a nonlinear Hall effect.
Current interests in KTO 2DEGs are focused on experiments that will test whether the superconductivity seen in KTO 2DEGs is of an unconventional nature.